e : le nombre d’Euler

Le nombre e est la base des logarithmes naturels, c’est-à-dire le nombre défini par ln(e) = 1. Cette constante mathématique, également appelée nombre d’Euler ou constante de Néper en référence aux mathématiciens Leonhard Euler et John Napier, vaut environ 2,71828.

• Remarques sur la fonction exponentielle et sur les fonctions logarithmes (parfois dites logarithmiques)

Certains enseignants en Mathématiques hésitent pour savoir s’ils doivent traiter la fonction exponentielle avant les fonctions logarithmes, ou le contraire. Personnellement, il me parait (beaucoup plus) évident de commencer par la fonction exponentielle, puis d’étudier la fonction ‘logarithme népérien’ comme la fonction ‘réciproque’ de la fonction exponentielle, puis de généraliser à l’ensemble des fonctions logarithmes.

> Approximation de la valeur de e en utilisant des racines ‘Nième’

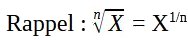
Il est possible d’obtenir de ‘bonnes’ approximations de e en utilisant la racine Nième de certaines valeurs, par exemples :

Facile à mémoriser : e = 20^1/3 … Mais aussi… 8103^1/9 ; 3269017^1/15 ; 178482301^1/19

> Approximation de la valeur de e en utilisant un développement limité à l’ordre n

On utilise le développement limité de la fonction e(x) :

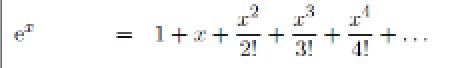
Plus précisément, on utilise le développement limité de e^x en prenant x=1 (car e¹ = e). On trouve alors :

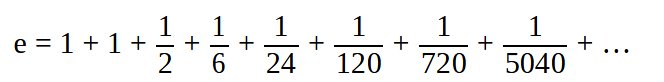
(Rappel : n! = 1*2*3* ….. *n)

> La fonction exponentielle

On considère qu’il existe une unique fonction f, dérivable sur IR, telle que : f'(x) = f(x) et f(0) = 1

On la nomme fonction exponentielle et elle est notée exp(x).

NB : La fonction exponentielle est donc définie ici par le biais d’une équation différentielle.

Nous avons : f'(x) = f(x) et f(0) = 1 , avec la notation exp(x)

Donc :

→ exp(0) = 1

→ exp est dérivable sur IR et exp'(x) = exp(x)

→ pour tout réel x, exp(x) > 0

→ la fonction exp est strictement croissante sur IR

• En termes de notation, on pose e = exp(1) et à l’aide de la calculatrice, on trouve e = 2,7182818284590452354…

e est nommé : nombre d’Euler, nombre exponentiel ou nombre de Neper

Par convention, on pose exp(x) = e^x pour tout réel x.

La fonction exponentielle est donc une fonction ‘puissance’ (elle va donc vérifier toutes les règles des opérations sur les puissances).

– Courbe représentative de la fonction exponentielle :

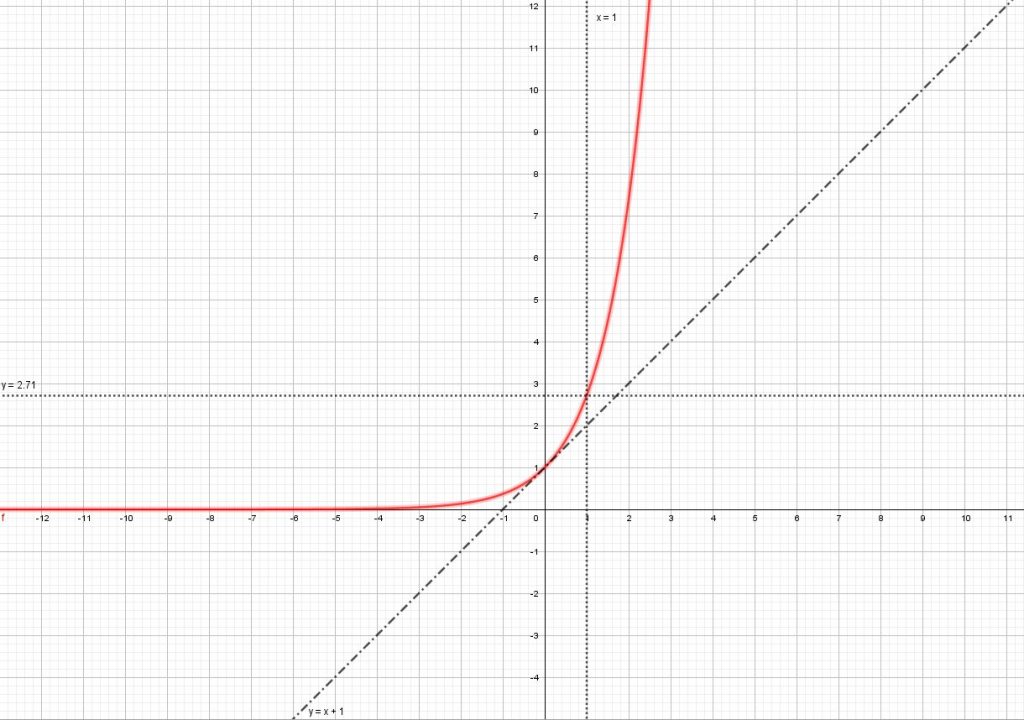
> Les fonctions logarithmes

Il existe une infinité de fonction logarithmes et toutes ces fonctions logarithmes possèdent des caractéristiques communes (que nous allons voir).

La principale fonction logarithme est la fonction ‘logarithme népérien’, notée Ln(x) et toutes les autres fonctions logarithmes peuvent se définir très facilement à partir de la fonction Ln(x).

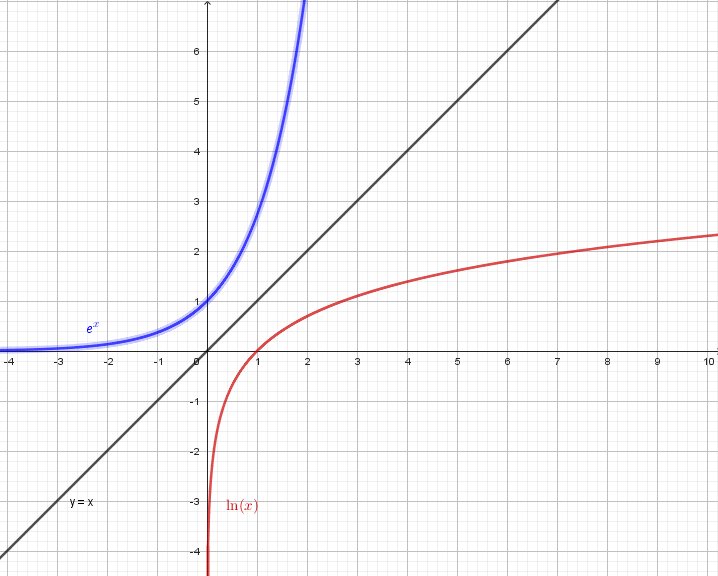
Pour construire la fonction logarithme népérien, notée ln(x), on considère qu’il s’agit de la bijection réciproque de la fonction exponentielle :

A savoir : pour tout x de R^+*, et pour tout y de R, ln(x) = y si et seulement si e^y = x

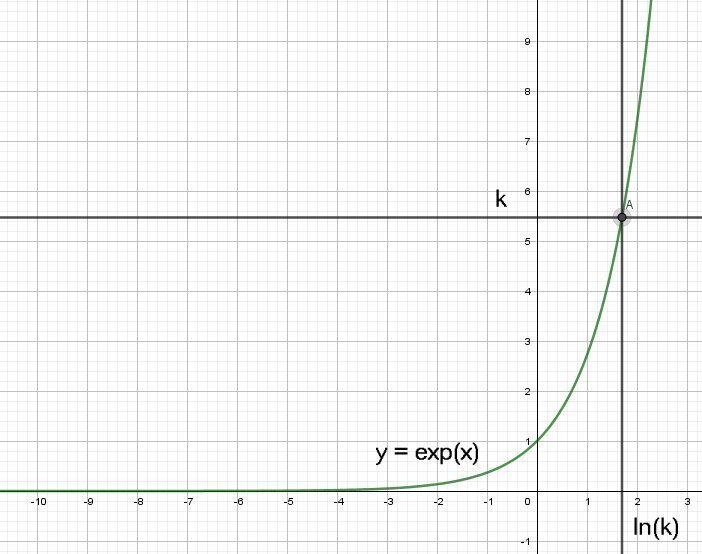
La courbe représentative de la fonction ln(x) se construit donc comme la courbe symétrique de la courbe représentative de la fonction e^x par rapport à la droite d’équation y = x

– Courbe représentative de la fonction ln(x) (en rouge)

– Relation entre puissances, exp et ln

A noter qu’il existe une relation directe entre la fonction puissance, la fonction exponentielle et la fonction logarithme népérien, en effet :

a^x = e^xln(a) (avec a > 0)

Par exemple : 3⁴ = e^4ln(3) ( = 81 )

– Généralisation à l’ensemble des fonctions logarithmes

On appelle fonction logarithme de base a (a appartenant à IR+* – {1} ) la fonction notée log_a définie par : log_a(x) = ln(x) / ln(a)

Cas particuliers :

a = e –> log_e(x) = ln(x) / ln(e) = ln(x) (cas du logarithme népérien)

a = 10 –> log₁₀(x) = ln(x) / ln(10) = log(x) (cas du logarithme décimal)

NB : par convention, si on ne précise pas de base pour une fonction log(x), cela signifie que nous utilisons le logarithme décimal.

Sachant que ln(10) = 2,302 ( valeur approchée de ln(10) ) , on en déduit que :

ln(x) = 2,302 log(x) et log(x) = 0,43 ln(x)

– Courbes représentatives des fonctions logarithmes

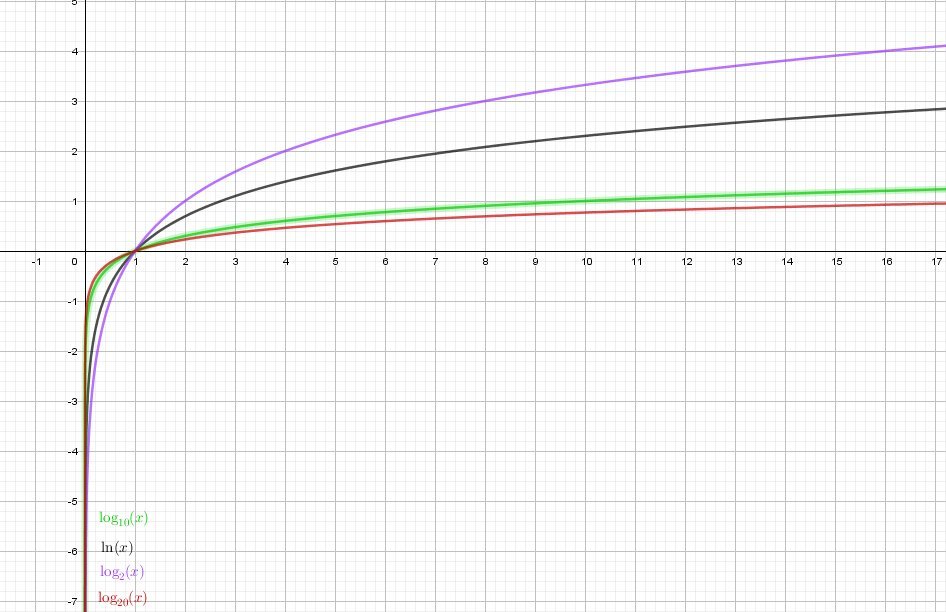
On voit que toutes les courbes sont similaires. elles passent toutes par le point de coordonnées (1; 0).

Par abus de langage, nous pouvons dire que les courbes sont plus ou moins ‘écrasées’, ce qui est logique car nous avons log_a(x) = ln(x) / ln(a) ; nous divisons donc par une valeur qui augmente en fonction de la valeur de a (a > 0).