Pour rappel, une suite numérique U est une fonction définie sur N (ensemble des entiers naturels), à valeurs dans R (ensemble des réels), qui à tout entier naturel n associe le nombre réel « U de n », aussi noté « U indice n ». Exemple d’une suite numérique : Un = 3*n + 2
NB : les suites numériques les plus simples et les plus ‘étudiées’ sont les suites arithmétiques et les suites géométriques.
Il est aussi possible de définir une suite numérique dont chacun des termes s’exprime par plusieurs termes précédents ; par exemple : Un+2 = Un+1 + Un
Dans ce cas, afin de pouvoir effectuer les calculs, il est nécessaire de définir les 2 premiers termes : U0 et U1
La suite (Un) définie par Un+2 = Un+1+ Un avec U0 = 0 et U1 = 1 est appelée suite de Fibonacci.
Leonardo Fibonacci (dit Léonard de Pise) était un illustre mathématicien italien du 13ème siècle.
La suite de Fibonacci est liée au nombre d’or, φ (phi). Rappelons que le nombre d’or est la racine positive de l’équation : x2 – x – 1 = 0 (voir la page traitant du nombre d’or).
Revenons à la suite de Fibonacci et énumérons ses premiers termes : 0, 1 , 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … (à chaque fois, il suffit d’additionner les deux termes précédents). Regardons maintenant une ‘représentation graphique’ de ces nombres …
> La spirale de Fibonacci (la spirale d’or)
Dans un 1er temps, nous allons dessiner une juxtaposition de carrés dont les côtés ont pour longueur les nombres successifs de la suite de Fibonacci : 1, 1, 2, 3, 5, 8, 13 et 21.
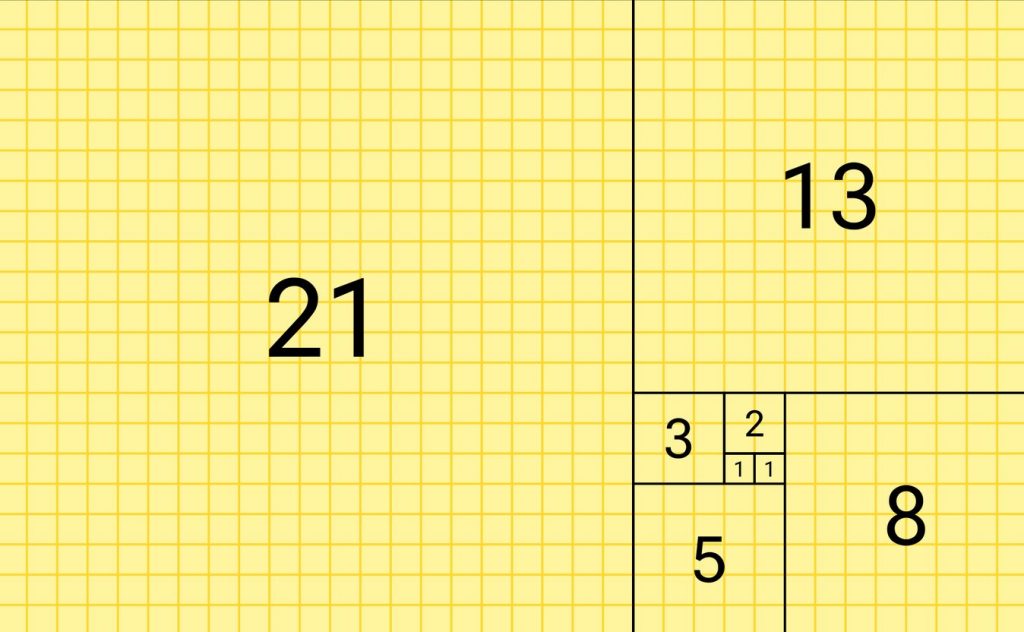
pour le dessin ci-dessus : Source Wikipédia : Romain, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
Explication de la construction du dessin précédent : à partir d’un carré central de côté 1, on construit un nouveau carré qui s’appuie sur le précédent. Puis on répète la construction, chaque nouveau carré appuie son côté sur l’ensemble des carrés déjà construits.
Ensuite, dans chaque carré, nous allons tracer un quart de cercle joignant un sommet au sommet opposé, de sorte que les quarts de cercle soient consécutifs. La courbe obtenue s’appelle la spirale de Fibonacci.
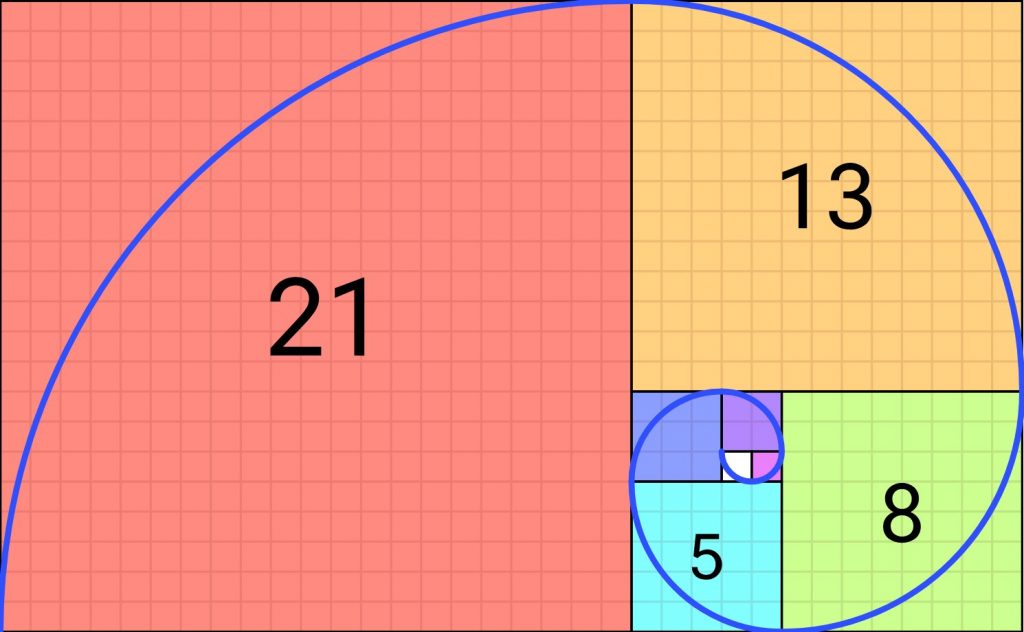
(Pour le dessin ci-dessus : Source Wikipédia)
Les termes de la suite de Fibonacci se retrouvent fréquemment dans la nature : sur les cônes de pin, les ananas, ou les fleurs de la famille des tournesols, on observe des motifs en forme de spirales, qui s’organisent en deux réseaux qui se croisent. Si la curiosité nous pousse à compter les spirales de ces réseaux, on obtient très souvent deux nombres consécutifs de la suite de Fibonacci. Par exemple sur un cône de pin on compte en général 8 spirales dans un sens et 13 spirales dans l’autre sens. Au cœur d’une marguerite ou d’un aster, les minuscules fleurs disposées sur le capitule (les fleurons) forment deux familles de 13 et 21 spirales, voire 21 et 34.
Nous retrouvons aussi cette spirale au fond des océans et dans l’univers …

Je profite de ces photos pour rappeler une belle citation de Gaston Bachelard (philosophe français des sciences, de la poésie, de l’éducation et du temps ; 1884/1962) : “Dès l’époque secondaire, les mollusques construisaient leur coquille en suivant les leçons de géométrie transcendante.”
> Calcul de π avec les valeurs de la suite de Fibonacci
J’ai précisé dans la page dédiée aux calculs d’approximations de la valeur de π que nous pouvons utiliser le développement limité de ArcTg(x) qui est la fonction ‘réciproque de la fonction tangente : tg(x) = sin(x)/cox(x)
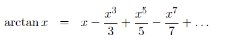
Pour rappel : tg(π/4) = 1 ; on en déduit que arctg(1) = π/4 ; pour calculer arctg(1) en utilisant le développement limité associé, nous utilisons tout simplement la formule précédente en remplaçant x par 1 :
Donc π/4 = arctg(1) = 1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + 1/13 – 1/15 + …
En utilisant le développement limité de arctg(x), on obtient : π = 4 * (1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + 1/13 – 1/15 + …)
–> Nous pouvons ‘généraliser’ cette formule en utilisant les nombres de la suite de Fibonacci, en effet, nous avons les égalités suivantes :
π/4 = arctg(1)
π/4 = arctg(1/2) + arctg(1/3)
π/4 = arctg(1/2) + arctg(1/5) + arctg(1/8)
π/4 = arctg(1/2) + arctg(1/5) + arctg(1/13) + arctg(1/21)
π/4 = arctg(1/2) + arctg(1/5) + arctg(1/13) + arctg(1/34) + arctg(1/55)
J’ai précisé que arctan(x) est la fonction ‘réciproque’ de tan(x) ; nous pouvons donc écrire la fonction arctan(x) sous la forme tan-1(x)
Si nous considérons la suite de Fibonacci avec ses différentes valeurs, Fi va représenter le ième terme de cette suite.
Nous obtenons alors la ‘généralisation’ :
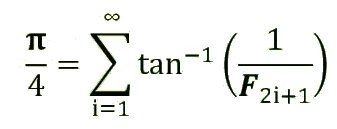
> Polynôme générateur des nombres de Fibonacci
Pour information, il existe un polynôme générateur des nombres de Fibonacci :
1/ (1 – x – x2) = 1 + x + 2x2 + 3x3 + 5x4 + 8x5 + 13x6 + …
Ce polynôme permet d’obtenir tous les nombres de Fibonacci (pour mieux visualiser TOUS les nombres, on peut écrire le polynôme précédent sous la forme : 0 + 1 + x + 2x2 + 3x3 + 5x4 + 8x5 + 13x6 + …
Je ne vais pas démontrer la justification de ce polynôme, mais je vous propose à titre d’information le calcul suivant :
(1 – x – x2 ) * (1 + x + 2x2 + 3x3 + 5x4) = 1 + x + 2x2 + 3x3 + 5x4 – x – x2 – 2x3 – 3x4 – 5x5 – x2 – x3 – 2x4 – 3x5 – 5x6)
= 1 + 0x + 0x2 + 0x3 + 0x4 – 8x5 – 5x6
A l’exception du ‘1’, on voit que tous les termes s’annulent au fur et à mesure. Si je n’avais pas arrêté le polynôme à 5x4, le terme suivant (8x5) aurait annulé les ‘x5 ‘ (et ainsi de suite).
