Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. C’est même un nombre transcendant, ce qui signifie qu’il n’existe pas de polynôme non nul à coefficients entiers dont π soit une racine.
Je ne vais pas tenter de rappeler ici toutes les formules dans lesquelles la valeur de π intervient … ce ne serait pas réaliste … mais je vais juste me contenter de rappeler 2 formules très simples :
- La circonférence d’un cercle = 2 * π * R (R étant le rayon du cercle)
- La surface d’un cercle = π * R * R ( = π*R2 )
Je profite de cette allusion au cercle pour rappeler une citation de Tom Stoppard (Dramaturge né en 1937) : “Le cercle est le plus long chemin d’un point au même point.”
Il existe de nombreuses ‘définitions’ de π , parmi les plus connues, on retrouve les 6 valeurs suivantes :
- Définition ‘géométrique’ : π = Circonférence du cercle / Diamètre du cercle
- Définition ‘analytique’ (voir formule de Leibniz-Grégory) :
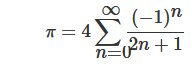
- Définition ‘trigonométrique’ :
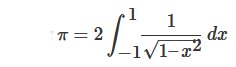
- Définition par fractions continues (formule attribuée à Ramanujan qui a aussi établi d’autres calcul de π) :
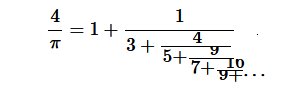
- Définition par la série de produits infinis de Wallis :
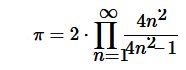
(Les premiers termes sont les suivants : 2 x ( 4/3 . 16/15 . 36/35 . 64/63 . 100/99 . 144/143 …. Notons qu’il faut ‘pousser’ le calcul relativement loin afin d’obtenir une approximation réaliste de π).
- Et enfin, une autre définition par fractions continues (William Brouncker) :
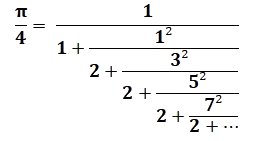
La valeur retenue la plus simple est généralement π = 3,14 … mais comme précisé précédemment π est irrationnel et comporte en fait une infinité de chiffres après la virgule … Nous allons donc regarder des formules permettant de calculer des approximations (pas trop fausses) de la valeur de π …
> Les célébrations de π
Rappelons aussi que π à son ‘jour’ : « The Pi Day », qui est tout simplement le 14 mars (écrit 3.14 en format de date américain).
Il existe même un site ‘officiel’ pour cette date : https://www.piday.org/
Dans le même domaine, rappelons aussi que π (avec sa journée) possède aussi sa ‘chanson’, il s’agit de « Oh! Happy Day » –> « Oh’ a Pi-Day » …
> Approximations ‘génériques’ de π
Voici une valeur de π avec une précision de plus de 50 chiffres après la virgule –> π = 3,14159265358979323846264338327950288419716939937510582
Euh … franchement, je suis incapable de retenir ces chiffres (de plus, nous allons rapidement dépasser la capacité de précision de nombreuses calculatrices …).
NB : Vous trouverez néanmoins en fin de page des moyens mnémotechniques permettant de mémoriser π avec un certain nombre de chiffres après la virgule.
Je ne vais pas (non plus) tenter de faire un historique complet (et exhaustif) de π (je pense que certains documents très anciens ont définitivement disparus …), mais n’oublions pas tout simplement que les premières calculatrices n’étaient pas dotées d’une touche ‘π’ et qu’il était donc nécessaire d’utiliser un calcul simple et facile à utiliser (et surtout à mémoriser) pour obtenir une approximation de π.
Cette valeur était 355/113 … valeur égale à 3,1415929204… donc fournissant une approximation de π avec 6 chiffres après la virgule … simple et très efficace !!!
NB : il existe bien entendu d’autres approximations ‘fractionnaires’ de la valeur de π ; parmi les plus connues, on trouve :
22/7 (=3,142857143) ; 333/106 (=3,141509434) ; 103993/33102 (=3,141592653) ; 104348/33215 (=3,141592654)
Voici maintenant quelques approximations de la valeur de π … Nous allons donc nous retrouver avec des calculs allant de « Pi en Pi » … Je vous rassure tout va bien se dérouler … loin de moi de vouloir intégrer une quelconque D’ … (Eh oui, je revendique les très mauvais jeux de mots de matheux ….).
L’une des plus anciennes approximations de π est en fait un ‘encadrement’ de sa valeur. Cet encadrement est (généralement) attribué à Archimède (-287 / -212) :
3 + 10/71 < π < 3 + 1/7 ; ce qui donne le calcul suivant 3,14084507 < π < 3,142857143 (approximation avec 2 chiffres après la virgule).
> Approximation de π en utilisant des racines ‘Nième’
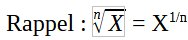
Il est possible d’obtenir de ‘bonnes’ approximations de π en utilisant la racine Nième de certaines valeurs, par exemples :
Facile à mémoriser : π = 311/3 …. mais aussi… 94891/8 ; 936481/10 ; 9242691/12
Les formules suivantes sont assez faciles à comprendre. A chaque fois, il est très facile d’écrire l’algorithme correspondant et d’écrire un petit programme permettant de réaliser le calcul associé (bien entendu, plus on ‘prolonge’ le calcul, meilleure sera l’approximation de la valeur de π) :
> Formule de Leibniz-Grégory :
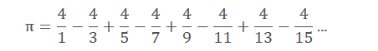
Alternance des signes + et – avec division du chiffre 4 par (tous) les nombres impairs successifs.
> Formule de Leibniz :
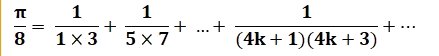
> Formule de Nilakantha :
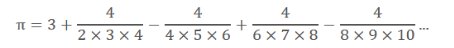
On part de 3, puis alternance des signes + et – avec division du chiffre 4 par les valeurs n*(n+1)*(n+2) ; plus particulièrement la valeur de n pour chacune des divisions correspond successivement aux nombres pairs. Pour être plus précis, on divise le chiffre 4 par les valeurs successives 2n*(2n+1)*(2n+2) pour n entier strictement positif.
> Les formules d’Euler :
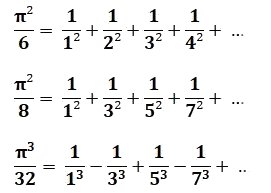
> Formule de Newton :
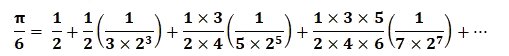
A noter : Il existe d’autres formule de π attribuées à Isaac Newton. D’autre part, cette formule converge rapidement ; on obtient en quelques termes une très bonne approximation de la valeur de π.
> Formule de Viète :
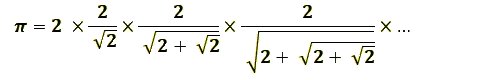
> Utilisation d’un développement limité :
Pour faire simple, l’usage d’un développement limité consiste à effectuer une approximation d’une fonction en la remplaçant par une fonction polynomiale.
Par exemple, il est possible d’approximer la fonction sinus(x) par une fonction polynomiale (son développement limité) :
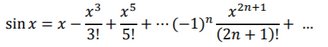
Pour calculer une approximation de la valeur de π, nous allons plus particulièrement utiliser le développement limité de ArcTg(x) qui est la fonction ‘réciproque de la fonction tangente ; pour rappel tg(x) = sin(x)/cos(x) [ sinus(x) divisé par cosinus(x) ]
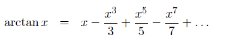
Rappelons que tg(π/4) = 1 car sin(π/4) = cos(π/4) ; on en déduit donc que arctg(1) = π/4
Pour calculer arctg(1) en utilisant le développement limité associé, nous allons tout simplement utiliser la formule précédente en remplaçant x par 1 :
Donc π/4 = arctg(1) = 1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + 1/13 – 1/15 + …
En utilisant le développement limité de arctg(x), on obtient : π = 4 * (1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + 1/13 – 1/15 + … )
(Alternance des signes + et – avec division du chiffre 1 par (tous) les nombres impairs ; le tout multiplié par 4).
> Formule de Machin
Il est aussi possible de calculer une valeur approchée de π par le calcul des développements limités à l’ordre n en utilisant la formule de Machin (John Machin en 1706) :
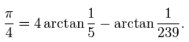
> Calcul de π utilisant la circonférence ‘approximative’ d’un cercle :
Nous allons utiliser ici un exemple de calcul simple permettant d’établir une approximation de π
Pour faciliter les calculs, nous allons prendre un cercle de rayon R = 1 mètre et nous allons découper ce cercle en 360 secteurs égaux. Nous définissons ainsi 360 triangles ayant 2 de leurs côtés faisant une longueur de 1 mètre.
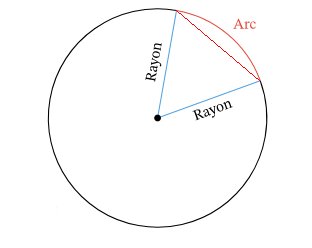
Nous allons ensuite considérer que la longueur du 3ème côté de chacun des triangles est ‘égale’ à la longueur de l’arc se trouvant le long de ce côté (d’où la nécessité de prendre un angle ‘très petit’ afin de pouvoir assimiler la longueur de ce 3ème côté à la longueur de l’arc correspondant (adjacent).
Pour rappel, dans un triangle quelconque, la formule d’Al-Kashi, nous indique que : a2 = b2 + c2 − 2bc cos(Â) Ici, nous avons b = c = 1 mètre et  = 1°
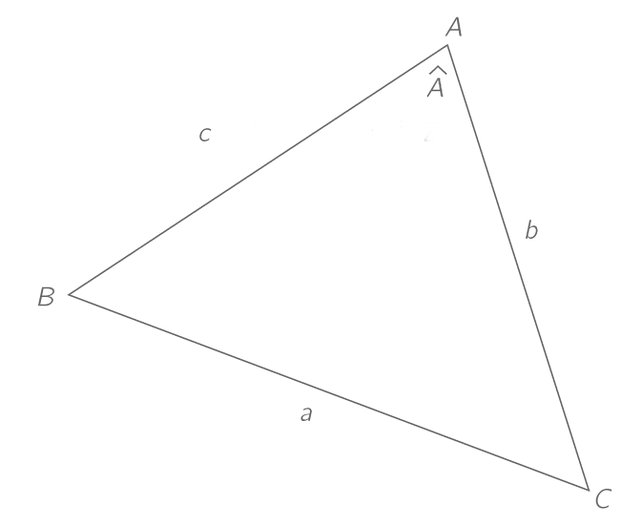
Ici, nous avons donc b = c = 1 mètre et  = 1° donc a2 = 12 + 12 − 2*1*1 cos(1°) –> a2 = 2 – 2 * 0,999847695 = 0,00030461 –> a = 0,017453071
Nous savons que la circonférence C d’un cercle est égale à 2 * π * R ; ici nous avons aussi (approximativement) C = 360 * a (car nous avons 360 secteurs égaux)
Donc, π = C / 2R = 360 * a / 2R = 180 * 0,017453071 = 3,14155278.
Par cette méthode nous trouvons π = 3,14155278 (donc avec une précision de 4 chiffres après la virgule).
> Autres méthodes :
Il existe bien entendu d’autres méthodes permettant d’obtenir une approximation de la valeur de π
Par exemple, en prenant la limite à l’infini de la fonction f(x) = x sin(180/x) (avec x en degrés)
Nous allons aussi voir qu’il est possible de calculer une approximation de la valeur de π en utilisant les valeurs de la suite de Fibonacci (voir la page ‘Suite de Fibonacci’). Nous verrons que cette méthode peut se décrire comme une ‘généralisation’ de la formule » π/4 = arctg(1) « .
> Mémorisation de π :
Pour finir ce chapitre, je vais rappeler ici des méthodes de mémorisation de la valeur de π (pour être plus précis, des méthodes fournissant des approximations de π avec un certain nombre de chiffres après la virgule …).
–> Le ‘piem’ de Maurice Decerf :
Un des moyens mnémotechniques pour se souvenir des premières décimales de pi consiste à retenir le poème de Maurice Decerf.
Ce type de poème s’appelle un ‘’piem’’, contraction de poème et de pi.
Le poème de Maurice Decerf, permet de retenir plus de 120 décimales de pi.
Il suffit de compter le nombre de lettres de chacun des mots utilisés afin de connaître la décimale correspondante.
Si vous ne souhaitez pas retenir l’intégralité de ce poème, le premier vers reste un excellent moyen pour retenir les 10 premières décimales de pi très rapidement (ce qui est souvent bien suffisant).
Notons que pour représenter le chiffre 0, le poète utilise un mot de 10 lettres.
Autre particularité, ce poème est écrit en alexandrins !
Voici le poème de Maurice Decerf :
Que j’aime à faire apprendre ce nombre utile aux sages ! 3 1 4 1 5 9 2 6 5 3 5
Immortel Archimède, artiste ingénieur, 8 9 7 9
Qui de ton jugement peut priser la valeur ? 3 2 3 8 4 6 2 6
Pour moi, ton problème eut de pareils avantages. 4 3 3 8 3 2 7 9
Jadis, mystérieux, un problème bloquait 5 0 2 8 8
Tout l’admirable procédé, l’œuvre grandiose 4 1 9 7 1 6 9
Que Pythagore découvrit aux anciens Grecs. 3 9 9 3 7 5
0 quadrature ! Vieux tourment du philosophe 1 0 5 8 2 9
Insoluble rondeur, trop longtemps vous avez 9 7 4 9 4 4
Défié Pythagore et ses imitateurs. 5 9 2 3 0
Comment intégrer l’espace plan circulaire ? 7 8 1 6 4 0
Former un triangle auquel il équivaudra ? 6 2 8 6 2 0
Nouvelle invention : Archimède inscrira 8 9 9 8
Dedans un hexagone ; appréciera son aire 6 2 8 0 3 4
Fonction du rayon. Pas trop ne s’y tiendra : 8 2 5 3 4 2 1 1 7
Dédoublera chaque élément antérieur ; 0 6 7 9
Toujours de l’orbe calculée approchera ; 8 2 1 4 8 0
Définira limite ; enfin, l’arc, le limiteur 8 6 5 1 3 2 8
De cet inquiétant cercle, ennemi trop rebelle 2 3 0 6 6 4 7
Professeur, enseignez son problème avec zèle ! 0 9 3 8 4 4
> Mémorisations non francophones
–> Exemples de phrases mnémotechniques en anglais :
Yes, I have a great statement to relate. 3 1 4 1 5 9 2 6
May I have a large container of coffee ? 3 1 4 1 5 9 2 6
How I wish I could recollect of circle round The exact relation Archimede unwound. 3 1 4 1 5 9 2 6 5 3 5 8 9 7
How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics! 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9
How I wish I could enumerate Pi easily, since all these horrible mnemonics prevent recalling any of pi’s sequence more simply. 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 (l’une de mes préférées en anglais avec ‘May I have a large container of coffee ?’ )
–> Exemples de phrase mnémotechniques en espagnol :
Con 1 palo y 5 ladrillos se pueden hacer mil cosas. 3 1 4 1 5 9 2 6 5 3 5
Sol y Luna y cielo proclaman al divino autor del cosmo. 3 1 4 1 5 9 2 6 5 3 5
