Dans cette page, je vais donner quelques exemples de ‘curiosités’ mathématiques.
(Il s’agit d’une petite sélection car il existe de très nombreux exemples de ce genre).
> Fonction ‘Merry Christmas’
Soit la fonction y = ln(x/m – sa) / r2
On multiplie par r2 , on obtient alors yr2 = ln(x/m – sa)
On prend l’exponentielle des 2 termes → eyr2 = x/m – sa
On multiplie ensuite par m → meyr2 = x – msa
On remplace r2 par rr , on obtient alors merry = x – msa ; on obtient donc :
merry = x – mas
(C’est à dire : merry X-mas)
> Une étrange suite de décimales
Des amateurs de mathématiques ont découvert quelque chose d’étrange concernant le nombre 998 001
En effet, si vous divisez le chiffre 1 par 998 001, ce qui suivra la virgule après une courte suite de «0» seront tous les nombres allant de un à trois chiffres possibles (soit de 0 à 999), excepté un seul !
Avec ce calcul, nous obtenons 1,002003004005006007…(10-6) et ainsi de suite jusqu’à 999.
Cependant, il manquera une valeur avant d’atteindre « 999 », et uniquement une seule ! Vous l’aurez probablement deviné : il s’agit du nombre « 998», qui fait étrangement penser à notre dénominateur « 998001 ».
Ce qui est d’autant plus étrange, c’est que le dénominateur nous donne un autre indice avec sa terminaison « 001 », qui n’est autre que la première suite de 3 chiffres du début de la série qui mène à 999.
Les mathématiques, c’est beau et parfois mystérieux… Et c’est ce qui les rend fascinantes ! N’est-ce pas ?
> Exemple de calcul erroné (1/3)
Nous partons de l’équation a = b
Ensuite, on multiplie par a → a2 = ab
Puis, on soustrait b2 → a2 – b2 = ab – b2
Nous voyons que d’un côté, nous avons une identité remarquable et de l’autre côté nous pouvons factoriser b → (a+b)(a-b) = b(a-b)
On simplifie ensuite par (a-b) → a + b = b
Comme nous avons a = b, on remplace a par b → b + b = b → 2b = b –> (2*b)= (1*b)
On simplifie alors par b et on obtient 2 = 1
Aberrant n’est-ce pas ?
> Exemple de calcul erroné (2/3)
Soit S = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + 1/7 – 1/8 + …
S = ( 1 – 1/2 – 1/4 ) + ( 1/3 – 1/6 – 1/8 ) + … + [ 1/(2n-1) – 1/2(2n-1) – 1/4n ] + …
S = ( 1/2 – 1/4) + ( 1/6 – 1/8) + … + [ 1/2(2n-1) – 1/4n ] + …
S = 1/2 ( 1 – 1/2) + 1/2 ( 1/3 – 1/4) + … + 1/2 [ 1/(2n-1) – 1/2n ] + …
S = 1/2 ( 1 – 1/2 + 1/3 – 1/4 + … + [ 1/(2n-1) – 1/2n ] + … )
Dans la parenthèse, on trouve l’expression de S
Donc S = 1/2 S –> 2S = S
Soit en simplifiant par S
2 = 1
> Exemple de calcul erroné (3/3)
Cette fois-ci, nous allons utiliser une intégrale avec une intégration par partie.
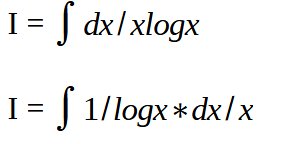
on pose u = 1 / logx et v’ = dx/x , ce qui nous permet de faire une intégration par partie (avec u’ = – 1/(xlog2x) et v = logx)
(Rappel (uv)’ = u’v + v’u = u’v + uv’ –> uv’ = (uv)’ – u’v ; ensuite on intègre termes à termes)
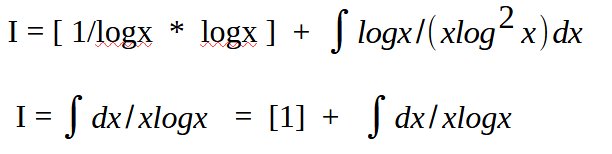
Nous trouvons donc I = 1 + I → 0 = 1
> Nombres amicaux et nombres parfaits
Eh oui, en mathématiques il existe des nombres (dits) amicaux et aussi des nombres (dits) parfaits …
2 nombres entiers positifs N et M sont dits amicaux (parfois on utilise aussi le terme ‘aimables’), si la somme des diviseurs de N (N non compris) vaut M et si la somme des diviseurs de M (M non compris) vaut N.
Exemple : 220 et 284
- Somme des diviseurs de 220 : 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
- Somme des diviseurs de 284 : 1 + 2 + 4 + 71 + 142 = 220
Autres exemples : 1184 et 1210 ; 17296 et 18416
Un nombre ‘parfait’ est un nombre qui est égal à la somme de ses diviseurs (excepté lui même), par exemple 6 = 1 + 2 + 3
Remarque : Un nombre parfait est amical avec lui même … on pourrait presque le qualifier de narcissique … mais, ce n’est pas si simple que cela car il existe en fait une définition pour les nombres narcissiques …
> Nombres narcissiques
Un nombre narcissique (ou nombre d’Armstrong) est un nombre qui est égal à la somme de ses chiffres élevés à la puissance du nombre de chiffres constituant ce nombre lui-même.
Très facilement, nous pouvons voir que tous les chiffres de 0 à 9 sont narcissiques, mais ensuite ça se complique ….
Les 10 termes suivants sont 153, 370, 371, 407, 1 634, 8 208, 9 474, 54 748, 92 727 et 93 084.
Par exemples :
153 = 13 + 53 + 33 = 1 + 125 + 27
8208 = 84 + 24 + 04 + 84 = 4096 + 16 + 0 + 4096
92727 = 95 + 25 + 75 + 25 +75 = 59049 + 32 + 16807 + 32 + 16807
> Nombre automorphe
Il s’agit d’un nombre n dont le carré n2 se termine par n.
Exemples : 52 = 25 ; 252 = 625 ; 762 = 5776
> Nombre carré gigogne
Il s’agit d’un carré pour lequel il existe un nombre, qui, inséré en son milieu donne à nouveau un carré (et l’opération peut se renouveler indéfiniment).
Exemples :
- 16 et 15 : 16 est le carré de 4 et nous allons pouvoir insérer le nombre 15 au milieu de chaque résultat et continuer à obtenir des carrés :
16 = 42
1 15 6 = 242
11 15 56 = 3342
111 15 556 = 33342
- 49 et 48 : 49 est le carré de 7 et nous allons pouvoir insérer le nombre 48 au milieu de chaque résultat et continuer à obtenir des carrés :
49 = 72
4 48 9 = 672
44 48 89 = 6672
444 48 889 = 66672
> Nombres premiers jumeaux
Deux nombres premiers sont jumeaux si leur différence est égale à 2
Exemples : (11 ; 13 ) ; (41 ; 43) ; (269 ; 271) ; (809 ; 811) ; …
A noter : à l’exception de (3 ; 5), tous les couples de nombres premiers jumeaux sont de la forme (6n -1 ; 6n + 1).
> Nombres étranges
Un nombre étrange est un entier naturel n qui est abondant mais non semi-parfait : la somme de ses diviseurs propres (y compris 1 mais pas n) est plus grande que n mais aucune somme de certains de ses diviseurs n’est égale à n.
Plus précisément :
– un nombre abondant est un nombre entier naturel non nul qui est strictement inférieur à la somme de ses diviseurs stricts ; autrement dit, c’est un entier n strictement positif tel que : 2n < σ(n)
où σ(n) est la somme des entiers positifs diviseurs de n (y compris n).
Par exemples :
Les diviseurs de 8 sont 1, 2 et 4 et nous avons (1+2+4) = 7 < 8. Donc 8 n’est pas un nombre abondant.
Par contre les diviseurs de 12 sont 1, 2, 3, 4, 6 et nous avons (1+2+3+4+6) = 16 > 12. Donc 12 est un nombre abondant.
– un nombre semi-parfait (ou nombre pseudoparfait) est un entier naturel non nul qui est égal à la somme de certains ou de tous ses diviseurs stricts.
Par exemple, 12 est semi-parfait car 12 = 1 + 2 + 3 + 6
– Un nombre étrange est donc un entier qui est abondant mais qui n’est pas semi-parfait.
Le plus petit nombre étrange est 70. Ses diviseurs propres sont 1, 2, 5, 7, 10, 14 et 35. Leur somme vaut 74 mais aucune somme de certains de ses diviseurs ne donne 70.
Les premiers nombres étranges sont : 70, 836, 4 030, 5 830, 7 192, 7 912, 9 272, 10 430.
Il est à noter qu’il existe une infinité de nombres étranges et que le produit d’un tel nombre avec un nombre premier assez grand est encore étrange.
> Comment j’ai détesté les maths
‘’Comment j’ai détesté les maths’’ est un (excellent) documentaire de 2013 réalisé par Olivier Peyon. Ce documentaire essaie de comprendre comment les maths en sont-elles arrivées à souffrir d’une telle désaffection alors qu’elles sont partout dans notre vie.
Parmi les personnes interviewées, on retrouve Cédric Villani (médaille Field 2010) qui partage (entre autres) cette réflexion en faisant 2 colonnes concernant les mathématiques, séparant ainsi les aspects ‘négatifs’ et les aspects ‘positifs’ de cette matière :
‘’Les mathématiques sont rigoureuses, oui, mais … imaginatives aussi.
Les mathématiques sont abstraites mais … universelles.
Les mathématiques sont inégalitaires et … démocratiques.
Elles sont anciennes et … en mutation permanente.
Elles sont solitaires et … sociales à la fois.
Elles sont difficiles et … simplissimes.
Alors quand on regarde toute la colonne de gauche, c’est assez dur :
rigoureux, abstrait, inégalitaire, ancienne, solitaire, difficile.
Mais la colonne de droite ça fait :
imaginatif, universel, démocratique, en mutation permanente, social, et simplissime.
Ah, c’est plus sexy !’’
