Le nombre d’or φ est une proportion initialement définie en géométrie entre 2 longueurs a et b telle que :
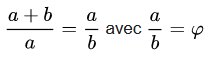
(Pour cette première définition, il s’agit donc d’une ‘définition géométrique).
Nous avons donc (a + b) * b = a * a donc ab + b2 = a2, donc a2 – ab – b2 = 0
En divisant par b2 , on obtient a2/b2 – a/b – 1 = 0, soit φ2 – φ – 1 = 0 (car a/b = φ).
On se retrouve avec une équation du second degré admettant 2 racines réelles (1 racine négative et 1 racine positive). Étant donné qu’il s’agit d’une proportion entre 2 longueurs, nous allons retenir uniquement la racine positive afin d’obtenir la valeur (exacte) de φ :
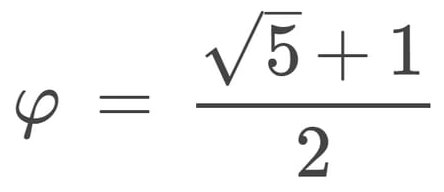
(Il s’agit donc ici d’une ‘définition algébrique).
Mais nous pouvons aussi donner 2 autres définitions du nombre d’or φ :
- Définition par fractions continues :
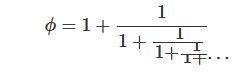
- Définition trigonométrique (donnant une 1ère relation entre φ et π) :
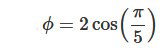
Une valeur approximative de φ généralement utilisée est φ = 1,618033989
> φ et son inverse
Nous avons φ2 – φ – 1 = 0 ; en divisant par φ, on obtient φ – 1 – 1/φ = 0 ; on obtient donc tout simplement 1/φ = φ – 1 ; soit 1/φ = 0,61803398…
> Approximations de φ et de 1/φ
Une bonne approximation de φ est φ = 377/233 (= 1,618025751) donc 1/φ = 233/377 (= 0,618037135)
> Approximation de φ en utilisant des racines ‘Nième’
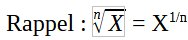
Il est possible d’obtenir de ‘bonnes’ approximations de φ en utilisant la racine Nième de certaines valeurs, par exemples :
Facile à mémoriser : φ = 1231/10 … mais aussi … 22071/16 ; 396031/22 ; 18604981/30
> Calcul de 51/2 en utilisant φ
(Rappel : élever un nombre à la puissance 1/2 revient à calculer sa racine carrée)
Très simplement, nous avons :
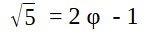
Mais aussi :
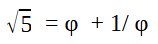
> Écriture de φ en utilisant (que) le chiffre 5 :
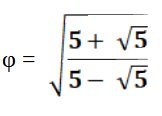
> Écriture avec un 5 et des 0,5
φ = 50,5 * 0,5 + 0,5
En écriture anglaise (anglo-saxonne), cette équation peut s’écrire exclusivement avec des 5 : φ = 5.5 * .5 + .5 (ou encore φ = 5^ .5 * .5 + .5 )
> Nombre d’or et suite de Fibonacci
Pour rappel, la suite (Fn) définie par Fn+2 = Fn+1+ Fn avec F0 = 0 et F1 = 1 est appelée suite de Fibonacci (voir la page sur la suite de Fibonacci).
Les premiers termes de cette suite ont pour valeurs : 0, 1 , 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Si nous considérons la suite de Fibonacci avec ses différentes valeurs , Fi va représenter le ième terme de cette suite (Attention : il serait en fait nécessaire de faire un décalage d’indice … en effet F0 est en réalité la 1ère valeur de cette suite).
La suite de Fibonacci intervient dans l’écriture des réduites de l’expression de φ en fraction continue. En effet, les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d’or : φ = Fn+1 / Fn (avec n différent de 0).
Par exemple, en prenant des valeurs successives de valeurs de la suite de Fibonacci : : 34/21 = 1,61904 ; 55/34 = 1,61764 ; 89/55 = 1,61818 ; 144/89 = 1,61797 ; 233/144 = 1,61805 …. On obtient très rapidement une valeur approximative (assez précise) du nombre d’or (par ‘oscillation’ autour de cette valeur).
NB : il existe une valeur appelée « Nombre d’argent » (noté φ2).
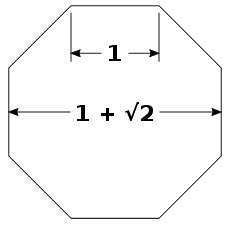
Par analogie avec le nombre d’or, φ2 peut être défini comme une proportion entre 2 longueurs a et b telle que :
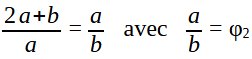
Nous avons donc (2a + b) * b = a * a donc 2ab + b2 = a2, donc a2 – 2ab – b2 = 0
En divisant par b2 , on obtient a2/b2 – 2a/b – 1 = 0, soit φ22 – 2φ2 – 1 = 0 (car a/b = φ2).
De la même manière que pour le nombre d’or, on se retrouve avec une équation du second degré admettant 2 racines réelles (1 racine négative et 1 racine positive). Étant donné qu’il s’agit d’une proportion entre 2 longueurs, nous allons retenir uniquement la racine positive afin d’obtenir la valeur (exacte) de φ2 :
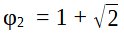
Une valeur approximative de φ2 généralement utilisée est φ2 = 2,414213562
Afin de ‘visualiser’ la construction du nombre d’argent, il suffit de regarder les proportions d’un octogone régulier (‘largeur’ vs ‘un côté’) :