Dans cette page, nous allons regarder la somme de tous les entiers naturels avec un calcul spécifique qui a été étudié par de nombreux grands mathématiciens.
Ce calcul va nous amener à estimer la ‘valeur’ de l’infini à -1/12 …
> Rappels
Avant de commencer ce calcul, je vais rappeler 2 points précis :
- Lorsqu’on additionne des entiers strictement positifs, le résultat est (théoriquement) strictement positif.
- La somme S des n premiers entiers est directement fournie par la formule S = n(n+1)/2
Par exemples :
pour n= 5 : 1 + 2 + 3 + 4 + 5 = 15 ( = 5*6 / 2 )
pour n = 10 : 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 ( = 10*11 / 2 )
> Étude de l’équation (E): 1 + 2 + 3 + 4 + 5 + 6 + 7 + …. = – 1/12
Dans cette équation, on prend en compte le fait qu’on additionne une ‘infinité’ de termes (tous les nombres entiers naturels), c’est à dire l’équation (E) revient à :
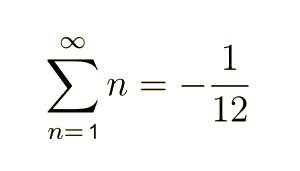
Évidemment, nous pouvons rapidement nous poser la question suivante : en additionnant une infinité de termes positifs, peut-on obtenir un résultat négatif ???
Cela peut paraitre assez absurde mais les lignes qui vont suivre vont vous étonner.
Voici donc les détails du calcul (en utilisant des étapes intermédiaires) …
> 1ère étape (en alternant des 1 et des -1 dans une addition)
Dans un 1er temps, nous allons regarder plus particulièrement la somme S1 = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 ….
Regardons maintenant la valeur de ( 1 – S1 )
( 1 – S1 ) = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 + …..
On remarque que l’expression de ( 1 – S1 ) est égale à S1.
On obtient donc 1 – S1 = S1 donc 1 = 2 * S1 donc S1 = 1/2
> 2ème étape (somme des entiers en alternant les signes et différents calculs)
Nous allons maintenant prendre en compte la somme S2 = 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 ….
Puis, nous allons calculer les valeurs de (S1 + S2) et aussi de (-1 + S1 + S2) …
Commençons donc par (S1 + S2) :
(S1 + S2) = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 ….
+ 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 ….
= 2 – 3 + 4 – 5 + 6 – 7 + 8 – 9 + 10 …..
Regardons maintenant (-1 + S1 + S2) …
(-1 + S1 + S2) = – 1 +( 2 – 3 + 4 – 5 + 6 – 7 + 8 – 9 + 10 …) = – 1 + 2 – 3 + 4 – 5 + 6 – 7 + 8 – 9 + 10 …..
on reconnait ici la série des termes de S2 avec -toutefois un signe opposé… Donc :
-1 + S1 + S2 = -S2
Ce qui nous donne -1 + S1 = -2S2 et nous avons démontré précédemment S1 = 1/2
donc -1 + 1/2 = -2S2 donc -1/2 = -2S2 donc S2 = 1/4
> 3ème étape (regardons maintenant notre somme initiale à laquelle nous allons soustraire S2)
Faisons le calcul ‘membres à membres’ pour les 2 lignes :
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11
-1 + 2 – 3 + 4 – 5 + 6 – 7 + 8 – 9 + 10 – 11
= 0 + 4 + 0 + 8 + 0 + 12 + 0 + 16 + 0 + 20 + 0 + …
= 4 + 8 + 12 + 16 + 20 + ….
= 4 (1 + 2 + 3 + 4 + 5 + …)
Concrètement si nous appelons notre somme initiale S ( S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + …), nous obtenons : S – S2 = 4S
Précédemment, nous avons calculé S2 = 1/4, donc S – 1/4 = 4S donc -1/4 = 3S –> S = -1/12
Nous obtenons donc : 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + … = -1/12
ce qui nous donne :
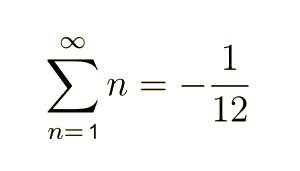
Nous démontrons ainsi qu’une somme infinie de termes strictement positifs est négative !!!!
> Réflexions et conclusion
Bon … OK, en fait, nous venons d’évaluer l’infini à -1/12 …. Ceci demande au moins une petite explication…
> L’hypothèse de Riemann
Derrière ce résultat paradoxal se cachent les fondements de ce qui est aujourd’hui considéré comme le plus grand problème mathématique jamais démontré : l’hypothèse de Riemann.
Nous pouvons aller encore plus loin dans cette démarche en utilisant la formule d’Euler-Maclaurin, les nombres de Bernoulli, la fonction zêta et la continuation analytique des variables réelles, mais je vais faire très simple … en mentionnant uniquement certains calculs connus afin de terminer sur une ‘généralisation’ …
Nous venons de montrer le calcul :
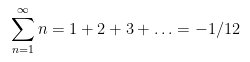
Mais nous pourrions aussi montrer de manière assez analogue :
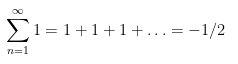
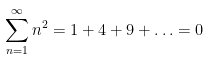
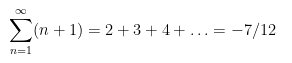
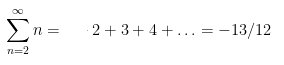
On voit que certains de ces résultats peuvent clairement paraitre en ‘contradiction’.
Rappel1 : nous avons vu que la somme des n premiers entiers est égale à n*(n+1)/2 ; rappelons aussi que la somme des n premiers entiers élevés au carré est égale à n*(n+1)*(2n+1)/6
Rappel2 : nous avons vu dans la page consacrée à π (parmi les formules d’Euler) que :
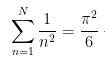
> Question non résolue
Pour finir ce chapitre, je vous fournis la question suivante qui n’a toujours pas été résolue : Quelles sont toutes les valeurs de x pour lesquelles, nous avons :
1x + 2x + 3x + 4x + 5x + 6x + 7x + … = 0
(Très) vaste sujet !!!!
